Plato's Analogy of the Divided Line

(Presented at the Eastern Division Meetings of the American Philosophical Association, December 1988.)

My aim in this essay is to suggest a reading of the divided line analogy in Republic (Rp) VI. I shall argue that the divided line should not be read either as depicting or as providing the basis for a scale according to which four categories of things can be arranged according to their respective levels of reality or truth. It is sometimes read in this way (e.g. by some of the commentators I shall refer to in section III), and it is understood as implying that for Plato the world of forms is in some strong sense separate from the world of perceptible things, and that our epistemic access to things is by means wholly distinct from those we use to grasp intelligible forms. I hope to cast doubt on these supposed implications. Properly to interpret the divided line analogy one must look back at the simile of the sun; I do this in section I. In section II I quote the passage in which the divided line analogy is drawn, Rp 509D6-511E5.[1] In section III I look closely at this passage, discuss what I take to be some common misreadings of it, and offer what I take to be a more nearly adequate reading. In section IV I discuss the relationship between the divided line analogy and the parable of the cave. In section V I turn briefly to Plato's notions of the visible and the intelligible "realms" [topoi] and ask whether they must be understood spatially or quasi-spatially, as suggesting that for Plato intelligible objects (things accessible to reasoning or understanding) occupy a different place or world than perceptible objects (things accessible to perception). I argue against taking Plato's two topoi in this way. In section VI I summarize my conclusions.

I

In Republic VI and VII Socrates repeatedly denies that he understands the form of the good, despite the fact that he describes it as "the most important thing to try to understand... because this is where anything that is moral (or whatever) gets its value and advantages from" (505A2-6; cf. 506C2-3, 506D6-8). The good, not surprisingly, is not to be identified with pleasure (505C6-D4); nor, perhaps surprisingly, is it to be identified with knowledge (505A6-C5). These denials do not discourage Glaucon from pressing Socrates for his own views about the good (506B2-C5). Socrates, having expressed his fear of disgracing himself and appearing ridiculous (506D7-8), suggests that for now they abandon the search for the good itself. He is prepared to talk about what seems to him to be the child of the good, something which bears a strong resemblance to it (506E3-4).

Socrates immediately reminds Glaucon of the distinction between the many beautifuls and many good things, on the one hand, and the beautiful itself [to auto kalon] and the good itself [to auto agathon], on the other (507B2-6; cf. 476A2, 479A3-5, 479E1-8, 480A11-12). Each of the latter is a single thing and properly referred to as "what really is" [ho estin] (507B7; cf. 476A5-7, 479E7-8; Phaedo 65D13-E1, 75D1-2). The former things are visible rather than intelligible, the latter intelligible rather than visible (Rp 507B9-10).

To see things one needs light, for which the sun is responsible; so while the sun is not sight itself, it is responsible for sight (507E4-508B10). The sun, then, is analogous [analogon] to the good:

As the good stands in the intelligible realm to intelligence and the things we know, so in the visible realm the sun stands to sight and the things we see [hotiper auto (sc. to agathon) en tôi noêtôi topôi pros te noun kai ta nooumena, touto touton (sc. ho hêlios) en tôi horatôi pros te opsin kai ta horômena]. (508B14-C2)

What makes visible objects visible, and what gives the eyes the power to see, is the sun; just so, Socrates suggests,

it's the good which gives the things we know their truth and makes it possible for people to have knowledge. It is responsible for knowledge and truth, and you should think of it as being within the intelligible realm, but you shouldn't identify it with knowledge and truth.... (508E1-5)

And the likeness [eikôn] can be pressed further: in the visible realm the sun not only gives visible things the ability to be seen, but it is also the source of their generation, growth, and nourishment -- though it isn't actually the process of generation (509B2-4). Likewise, Socrates says,

it isn't only the known-ness of the things we know which is conferred upon them by the good, but also their reality and their being, although goodness isn't actually the state of being, but surpasses it in majesty and might. (509B6-10)

So the good rules over the intelligible realm and its inhabitants [basileuein to men noêtou genous te kai topou], the sun over the visible [to d' horatou] (509D2-3). This contrast between these two forms [eidê, 509D4], the visible and the intelligible, serves as the backdrop for the divided line analogy.

II

The divided line analogy is developed at 509D6-511E5. It will be useful to have the whole passage before us:

"Well, picture them [sc. the visible and intelligible realms] as a line cut into two unequal sections and, following the same proportion, subdivide both the section of the visible realm and that of the intelligible realm. Now you can compare the sections in terms of clarity and unclarity. The first section in the visible realm consists of likenesses, by which I mean a number of things: shadows, reflections (on the surface of water or on anything else which is inherently compact, smooth, and bright), and so on. Do you see what I'm getting at?" (509D6-510A3)

"I do."

"And you should count the other section of the visible realm as consisting of the things whose likenesses are found in the first section: all the flora and fauna there are in the world, and every kind of artifact too." (510A5-7)

"All right."

"I wonder if you'd agree," I said, "that truth and lack of truth have been the criteria for distinguishing these sections, and that the image stands to the original as the realm of beliefs stands to the realm of knowledge?" (510A8-10)

"Yes," he said, "I certainly agree."

"Now we have to look at how to subdivide the section which belongs to the intelligible realm." (510B2-3)

"How?"

"Like this. If the mind wants to explore the first subdivision, it can do so only by using those former originals as likenesses and by taking things for granted on its journey, which leads it to an end-point, rather than to a starting-point. If it wants to explore the second subdivision, however, it takes things for granted in order to travel to a starting-point where nothing needs to be taken for granted, and it has no involvement with likenesses, as before, but makes its approach by means of forms alone, in and of themselves." (510B4-11)

"I don't quite understand what you're saying," he said.

"You will if I repeat it," I said, "because this preamble will make it easier to understand. I'm sure you're aware that practitioners of geometry, arithmetic, and so on take for granted things like numerical oddness and evenness, the geometrical figures, the three kinds of angle, and any other things of that sort which are relevant to a given subject. They act as if they know these things, treat them as basic, and don't feel any further need to explain them either to themselves or to anyone else, on the grounds that there is nothing unclear about them. They make them the starting-points for their subsequent investigations, which end after a coherent chain of reasoning at the point they'd set out to reach in their research." (510C1-D3)

"Yes, I'm certainly well aware of this," he said.

"So you must also be aware that in the course of their discussions they make use of visible forms, despite the fact that they're not interested in the visible forms as such, but in the things of which the visible forms are likenesses: that is, their discussions are concerned with what it is to be a square, and with what it is to be a diagonal (and so on), rather than with the diagonal (and so on) which occurs in their diagrams. They treat their models and diagrams as likenesses, when these things have likenesses themselves, in fact (that is, shadows and reflections on water); but they're actually trying to see squares and so on in themselves, which only thought can see." (510D5-511A1)

"You're right," he said.

"So it was objects of this type that I was describing as belonging to the intelligible realm, with the rider that the mind can explore them only by taking things for granted, and that its goal is not a starting-point, because it is incapable of changing direction and rising above the things it is taking for granted. And I went on to say that it used as likenesses those very things which are themselves the originals of a lower order of likenesses, and that relative to the likenesses, the originals command respect and admiration for their distinctness." (511A3-10)

"I see," he said. "You're talking about the objects of geometry and related occupations."

"Now, can you see what I mean by the second subdivision of the intelligible realm? It is what reason grasps by itself, thanks to its ability to practice dialectic. When it takes things for granted, it doesn't treat them as starting-points, but as basic in the strict sense -- as platforms and rungs, for example. These serve until it reaches a point where nothing needs to be taken for granted, and which is the starting-point for everything. Once it has grasped this starting-point, it turns around and by a process of depending on the things which depend from the starting-point, it descends to an end-point. It makes absolutely no use of anything perceptible by the senses: it aims for forms by means of forms alone, in and of themselves, and it ends its journey with forms." (511B2-C3)

"I don't quite understand," he said. "I mean, you're talking about crucial matters here, I think. I do understand, however, that you want to mark off that part of the real and intelligible realm which is before the eyes of anyone who knows how to practice dialectic as more clear than the other part, which is before the eyes of practitioners of the various branches of expertise, as we call them. The latter make the things they take for granted their starting-points, and although they inevitably use thought, not the senses, to observe what they observe, yet because of their failure to ascend to a starting-point -- because their inquiries rely on taking things for granted -- you're saying that they don't understand these things, even though they are intelligible, when related to a starting-point. I take you to be describing what geometers and so on do as thinking rather than knowing, on the grounds that thinking is the intermediate state between believing and knowing." (511C4-D5)

"There's nothing wrong with your understanding," I said. "And you should appreciate that there are four states of mind, one for each of the four sections. There's knowledge for the highest section and thought for the second one; and you'd better assign confidence to the third one and conjecture to the final one. You can make an orderly progression out of them, and you should regard them as possessing as much clarity as their objects possess truth." (511D6-E4)

"I see," he said. "That's fine with me: I'll order them in the way you suggest."

III

The basic ideas expressed in this passage are clear enough, but the details, and their implications for Plato's thought, are notoriously controversial. We are to imagine a line segment AB divided into unequal sections AC and CB; each of the segments is further divided in the same ratio, giving us AD and DC within AC and CE and EB within CB:

Figure 1.

AC is the visible section of the line, CB the intelligible. Within AC Plato distinguishes the contents of AD, which he calls likenesses (509E1), from those of DC, those things of which these likenesses are likenesses, the perceptible things around us (510A5-7). Within CB Plato appears to distinguish the contents of CE, which he at one point calls visible forms (510D5), from those of EB, the forms themselves (511C2). Finally, Plato also says that for each of these subsections of the line there is a state of mind: knowledge [noêsis] for EB, thought [dianoia] for CE, confidence [pistis] for DC, and conjecture [eikasia] for AD (511D6-E2). These four states of mind are said to be as clear as their objects are true (511E2-4).

What are we to make of all this? Plato's remarks at 509D6-511E5 fall naturally into two unequal parts, the first comprising 509D6-510B1, the second 510B2-511E5. In each part Plato describes a proportion like those used by practicing geometers, of the general form W : X :: Y : Z. (He has just constructed such a proportion, relating the good and the intelligible realm to the sun and the visible realm, at 508B14-C2 (quoted above, near the beginning of Section I). Notice also the repeated mention of geometrical practice at 509D6-7 and 510C2-511A1.) The first part (509D6-510B1) presents a proportion whose point is primarily ontological (it concerns the truth or reality of things). The second part (510B2-511E5) presents another proportion, whose point appears to be epistemological (it concerns the respective clarity of states of mind). Rather than making a single point in terms of a single line or a linear progression, I take Plato to be making two closely related points, each based on a different proportion. I shall devote the rest of this section to fleshing out these suggestions.[2]

To construct the first proportion we must distinguish these things:

1. likenesses or images [eikones, homoiôtha], such as shadows or reflections (509E1, 510A10);

2. the originals of these likenesses or images, i.e. "all the flora and fauna there are in the world, and every kind of artifact too" (510A5-6; cf. 510B4);

3. "the realm of beliefs" [ta doxasta, things grasped by doxa] (510A9);

4. "the realm of knowledge" [ta gnôsta, things grasped by gnôsis] (510A9).

The first proportion is (1) : (2) :: (3) : (4) (hôs to doxaston pros to gnôston, houtô to homoiôthen pros to hôi hômoiôthêi, 510A9-10). In the terms of Figure 1, AD contains likenesses -- shadows, reflections, and the like. In DC are the originals of those images, the perceptible things around us. Plato's claim is that these images are to their originals as "the realm of beliefs" [ta doxasta] is to "the realm of knowledge" [ta gnôsta]; i.e. AD : DC :: AC : CB. This clearly recalls the sun simile (ta gnôsta here corresponds to the "intelligible realm" [noêtos topos], ta doxasta to the "visible realm" [horatos topos]), and it echoes the terms of Plato's arguments against the sightlovers and soundlovers at 475E2-480A12. The point is an ontological one: "truth and lack of truth [alêtheiai te kai mê] are the criteria for distinguishing these sections" (510A8-9). Shadows and reflections (and likenesses generally) are not as true or as real as their originals (see 596E4-598D5 and Section VI below). Their existence and character as likenesses depends on that of their originals. Analogously, ta doxasta is not as true or as real as ta gnôsta. (This point is made throughout the Republic, most recently at 476B4-479E8; it is returned to later at 515C3-E5 and again at 596A5-598A2.) The point is perhaps obscured by the fact that the contents of (2), the perceptible things around us of which shadows and reflections are likenesses, cannot themselves be fully understood as such, since they contain opposing forms and so appear to us as confused and contradictory (see Rp 479A5-C5, 523C4-524D4; cf. Phaedo 74B7-C2). As we know from Republic V and elsewhere, only the forms as such can be fully understood.

Notice that at 509D6-8 AB is divided into AC and CB, and then AC and CB are divided "following the same proportion" into AD and DC, and CE and EB. It follows, of course, that DC = CE. W.D. Ross has suggested that Plato was unaware of this consequence of his proportion.[3] This is hard to believe. Why else would Plato insist that the initial line and both sections be divided in the same ratio? Besides, Plato draws attention to the fact that the same things that were originals in DC are used as likenesses in CE [hôs eikosin chrômenoi, 510B4-5, 510E3, 511A5-7]. I shall return shortly to some of the implications of the fact that DC = CE. At this point it is important to note only that although it follows from the proportion as he draws it that CE : EB :: AC : CB, Plato shows no interest in this fact at this point. The part of the passage in which the ontological proportion is drawn ends abruptly without any mention of the fact that not only is the ratio between the two visible terms (AD, DC) analogous to that between the visible and the intelligible (AC, CB), but the ratio between the two intelligible terms (CE, EB) is as well.[4]

To construct the second proportion we must distinguish four more things:

5. eikasia (conjecture, imagination) (511E2);

6. pistis (confidence, belief, conviction) (511E1);

7. dianoia (thought, reasoning) (511D4, 511D8);

8. nous or noêsis or epistêmê (knowledge, understanding, intellectual grasp) (511D4, 511D8).

The second proportion is (5) : (6) :: (7) : (8) (511D6-E4). I take Plato's point here to be epistemological (or psychological): the terms in this proportion are conditions [hexeis, 511D4] or states of mind [pathêmata en têi psuchêi, 511D7], and they are related to each other with respect to their degree of clarity [saphêneia, 511B1, 511C3, 511D5]. Plato is here contrasting the epistemic and psychological states that accompany and result from two kinds of reasoning, one which occurs in the visible section of the line, the other in the intelligible. He says much more about the intelligible section, so let me begin there.

Dianoia and noêsis differ in their uses of and attitudes toward hypotheses, "things taken for granted." Both offer us access to what is intelligible, as opposed to what is perceptible. A practicing geometer or mathematician, working with visible lines and figures, is thinking about the square itself and the diagonal itself, which are not visible (510D5-E1). The visible forms with which he works are useful as images in coming to see truths about intelligible objects (510E1-511A1). Now there are two attitudes one can take to the numbers, lines, angles, and figures of the mathematician. One is to take them as known [hôs eidotes, 510C6], as starting-points or first principles [archai, 511B5], and to reason from them without ever examining them. This is the customary attitude (510C2-D4), which involves reasoning from hypotheses to end-points or conclusions (510B4-6, 511A3-8). But then what one is entitled to conclude can be only as clear as one's hypotheses will allow; and since they are never themselves examined, this may leave room for unclarity or doubt. The state or condition of such a person is dianoia, "thought."

Another attitude is possible, however. Suppose one regards hypotheses not as starting-points, but as what they really are, hupo-theseis, things set down at the beginning of an inquiry to enable one to work one's way toward something else. This is what the dialectician does (511B3-C2). He begins with hypotheses just as the geometer does (510B7), but by subjecting his hypotheses to dialectical examination he can work his way to a clearer grasp, nous, of even the geometer's conclusions (511C8-D2). By diligent use of dialectic, Plato suggests, one can even work one's way to what is unhypothesized, the starting-point for everything (511B4-7). Having got that far, one can draw conclusions, even mathematical and geometrical ones, without using anything perceptible at all, but simply "by means of forms alone, in and of themselves, and [ending] with forms" (511B8-C2, 511C8-D2). The ideal here, as we know from Book VII, is twofold. First, one must get beyond reliance on the senses (537D5-8; cf. 522C6-525B3) -- hence astronomy becomes celestial kinematics (529A9-530C3) and harmonics becomes number theory (530E5-531C4). Second, and what Plato is concerned to stress here, one must not rely on unexamined hypotheses, but must subject all one's hypotheses to dialectical scrutiny. (Not at the same time, of course.) The dialectician, as distinguished from the practicing scientist or mathematician, sees things whole, and leaves no assumption unexamined (532A1-534B5, 537B8-C7). (It is in this sense that dialectic does away with, or uproots, hypotheses [tas hupotheseis anairousa, 533C8].) The state or condition of such a person is noêsis or nous or epistêmê, "knowledge" or "understanding."

Analogous to this contrast between dianoia and noêsis, both of which involve what is intelligible, is the contrast between eikasia and pistis, both of which involve what is perceptible. In eikasia one likens one thing to another, infers one thing from another on the basis of comparison or analogy, takes one thing as a likeness or image of another. One proceeds conjecturally, tentatively, in a sense indirectly, using one thing to get at another. (This is why eikasia is better translated as "conjecture" than as "imagination.") Shadows and reflections are likenesses of perceptible things (510A1-6). A perceptible thing is not only truer or more real (510A9-10), it is clearer than its shadow or reflection (511A6-8). The state or condition of one who confronts perceptible things directly, then, by aisthêsis, is clearer -- epistemically more perspicuous and reliable -- than that of one who gets at them by way of their shadows or reflections. If what you are after is clarity, it is usually better to study a tree or a frog than a picture -- much less a shadow or a reflection -- of a tree or a frog. Pistis, "confidence" or "conviction," is Plato's name for the state or condition of one who confronts perceptible things directly.[5] The state or condition of one whose access to perceptible things is only conjectural, by way of images, is eikasia. Hence the relation between eikasia and pistis is in this respect like that between dianoia and noêsis: in the former case one's access to something is indirect, in the latter it is direct. And with this difference, Plato suggests, comes a difference in clarity. Noêsis is clearer than dianoia, for the same reasons that pistis is clearer than eikasia.

So far, then, we have something like this:

Ontological Proportion
(1) likenesses [AD] : (2) originals [DC] :: (3) ta doxasta [AC] : (4) ta gnôsta [CB]

Epistemological Proportion
(5) eikasia [AD] : (6) pistis [DC] :: (7) dianoia [CE] : (8) noêsis [EB]

How, if at all, are these proportions related?

It might be objected, on the basis of 511E2-4, that Plato himself says or implies that there is a one-to-one correspondence between the terms of the second proportion (the states of mind) and those of the first (images, originals, etc.), and therefore that for each state of mind there is a unique ontological correlate. Plato would thus be committed to the view that the objects of noêsis or epistêmê [ta noêta] are necessarily different from those of dianoia [ta dianoêta]; that both are necessarily different from those of pistis [ta pista]; and that all three are necessarily different from those of eikasia [ta eikasta]. On this view, no object over which one of the epistemic states is set can be an object of any of the other epistemic states. If this were true, then Plato could be taken as offering only one scale or progression (albeit differently described) after all.

Is it true? I shall argue that it is not, beginning with a look at a number of passages within the divided line analogy. At 511D6-8, recalling Glaucon's reference to the state [hexis] of geometers and their kind, Socrates says that there are four such states of mind, set over or against the four subsections of the line [epi tois tettarsi tmêmasi tettara tauta pathêmata en têi psuchêi]. Each of the states he goes on to mention -- noêsis, dianoia, pistis, eikasia -- is set over a subsection of the line: noêsis is set over EB, dianoia over CB, pistis over DC, and eikasia over AD (511D8-E1). Further, noêsis, dianoia, pistis, and eikasia are graduated in clarity as what they are set over [eph' hois] varies in truth or reality (511E2-4). What are we to make of this?

It is possible, of course, that "subsections of the line" is functioning elliptically here, and that what Plato means to say is (a) that over the contents of each of the four subsections of the line there is set a (different) state of mind, and (b) that each subsection of the line contains a different kind or category of object. Thus noêsis would be set over the contents of EB; dianoia would be set over the contents of CE, and so on: for each epistemic state there would be a unique ontological correlate.

Socrates can plausibly be supposed to have provided Glaucon with a couple of examples of the contents of EB -- the square itself and the diagonal itself (510D7-8). Examples of the contents of AD presumably include the shadows and reflections mentioned at 509E1-510A3. The contents of DC presumably include perceptible things around us: flora, fauna, and artifacts (510A5-6). But what about the contents of CE? Socrates suggests, and Glaucon agrees, that practicing geometers make use of visible forms [tois horômenois eidesi proschrôntai] (510D5) -- and that these perceptible figures are likenesses of the forms themselves, which only dianoia can see (510E1-511A1). Unfortunately, this language obscures more than it clarifies. The forms themselves -- the contents of EB -- are supposed to be objects of noêsis, not of dianoia. Visible forms are the originals of which shadows and reflections in water are images (510E1-511A1). That is to say, they are perceptible, and as such they belong in DC, not in CE. Plato makes it very clear that one and the same thing (a visible triangle) can serve both as an original (when compared to the shadows and reflections that are the contents of AD) and as an image (when compared to the triangle itself, which is among the contents of EB). The fact is that Glaucon is given no clear sense of the contents of CE. Plato's point about the relations between noêsis and dianoia does not require this.

A few lines earlier, at 511C3-6, Glaucon draws a distinction between "that part of the real and intelligible realm which is before the eyes of anyone who knows how to practice dialectic" [to hupo tês tou dialegesthai epistêmês tou ontos te kai noêtou theôroumenon], and "the other part, which is before the eyes of practitioners of the various branches of expertise, as we call them" [to hupo tôn technôn kaloumenôn], and suggests that the former is clearer [saphesteron] than the latter. Here again it is possible that he is speaking elliptically: the objects of dialectic (i.e. the contents of EB) are clearer than the objects of the various branches of expertise (the contents of CE). But in the next several lines (511C6-D5), Plato ignores the supposed differences between the objects of dialectic and those of the various branches of expertise, and focuses entirely on the difference in method and attitude between the dialectician and the mathematician. He even insists that nous (i.e. noêsis) can be had of those things the practicing mathematician grasps by dianoia (511D1-2).

Similar things can be said of 510B2, where Plato begins to divide the intelligible section (CB) [tên tou noêtou tomên]. The division between the two sections is not made by reference to their respective contents or objects; here again Plato's interest is in the attitudes and methods characteristic of the intelligible subsections.

Finally, at 534A5-8, in a passage looking back at the line, Plato refers to what his four epistemic states -- epistêmê, dianoia, pistis, eikasia -- are set over [eph' hois], and hints that what they are set over, "the domain of belief" [to doxaston] and "the domain of intellect" [to noêton][6] can be divided into two; but he deliberately stops short of describing these interrelations, claiming that such a discussion would involve "an argument many times as long as the ones our discussion has already thrown up" [pollaplasiôn logôn]. If Plato thought that for each epistemic state there was a unique ontological correlate, why would lengthy arguments be needed to articulate this? If he thought this, it would be easy to say so; but Plato is careful to say nothing more than what he has already said at 511D6-E4.

None of the Platonic passages I have noted suggests that for each term in the epistemological proportion there is a corresponding term in the ontological proportion. My second reason for not reading Plato in this way requires a look at the sorts of proportions Plato gives us. As we have seen, if AC and CB are divided in the same ratio as AB, it follows that DC = CE. I suggested earlier that Plato is aware of this fact. So his first proportion is of the sort Greek mathematicians called "continuous." Aristotle distinguishes continuous and non-continuous (or separated) proportions thus:

Proportion is equality of ratios [analogia isotês esti logôn], and involves at least four terms. (It is obvious that the non-continuous [proportion] [hê diêremenê] has four terms; but so does the continuous [hê sunechês], since it treats the one as two and mentions it twice, e.g. "as line A is to line B, so B is to C." B is referred to twice, and if B is counted twice there will be four terms in the proportion.) (Nicomachean Ethics 1131a31-b2)

A similar distinction is assumed in Books V and VIII of Euclid's Elements, though Euclid does not draw it in the same terms as Aristotle.[7] As Thomas Heath notes in commenting on Elements VII Definition 20, "in the continuous proportion the consequent of one ratio is the antecedent of the next; in the separated proportion this is not so."[8] This is a signal difference between the proportions 2 : 4 :: 4 : 8 and 2 : 4 :: 5 : 10.

Plato's point is made with a line, not with a pair of numerical ratios. But this is what we should expect given the predominantly geometrical (i.e. non-arithmetized) nature of the mathematics of Plato's (and Euclid's) day.[9] If Euclid had wanted to express the fact that 2 : 4 :: 4 : 8, he would have drawn two unequally divided line segments, thus:

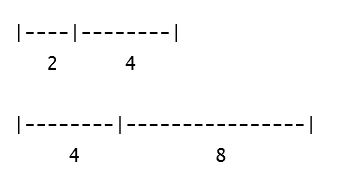
Figure 2.

(See Elements V, passim.) The two segments nicely express the desired proportion. At the beginning of the divided line passage (509D6-8), immediately before drawing the ontological proportion, Plato in effect places two such segments end to end, thus:

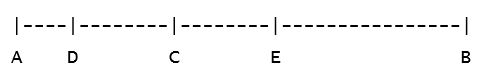
Figure 3.

Now it is evident both that AD : DC :: CE : EB, and also that AC : CB in the same ratio. In Plato's account AC is the visible section and CB the intelligible, each of which comprises two subsections; by putting the two sections end to end Plato can make two points with a single illustration, namely that the ratio between the visible and the intelligible sections (AC : CB) is equal to that between the first and second subsections of the visible (AD : DC) and to that between the first and second subsections of the intelligible (CE : EB). With respect to truth and falsity the contents of AD are to those of DC as the contents of AC are to those of CB. As we saw earlier, Plato is interested at 509D6-510B1 only in the proportion AD : DC :: AC : CB, and the other half of the story, CE : EB :: AC : CB, goes untold. Nevertheless, Plato suggests later that in CE the mind "uses as likenesses those very things which themselves are the originals of a lower order of likenesses" (511A6-7). In CE the mind uses the same things; but they are now -- in the intelligible section of the line, or from the point of view of their intelligibility -- used as likenesses (cf. 510B4-5, 510E3). The same things are treated as visible models in DC and as intelligible likenesses in CE. Treated as visible they are ta doxasta, and, more specifically, ta pista; treated as intelligible they are ta dianoêta. So, since in the ontological proportion the middle terms of AD : DC :: CE : EB are the same, the proportion is continuous.

Now consider the second (epistemological) proportion, developed at 510B2-511E4, and according to which the relation between dianoia and noêsis is analogous to that between eikasia and pistis (see especially 510C1-D4, 511B3-C1). Here are four different epistemic or psychological states, and Plato's claim is that eikasia : pistis :: dianoia : noêsis. Notice that this proportion cannot properly be thought of as equivalent to or isomorphic with the first, since unlike the first its middle terms are different. Consider the two ratios 2 : 4 and 5 : 10, i.e.

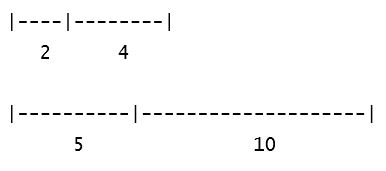
Figure 4.

The equality of these two ratios can be expressed as a proportion; we need only place the segments in Figure 4 end to end, thus:

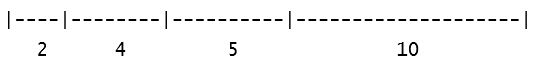
Figure 5.

It is true that 2 : 4 :: 5 : 10, but it is not true that (2 + 4) : (5 + 10) in the same ratio (contrast Figure 3 above). A non-continuous proportion like that in Figure 5 behaves quite differently than a continuous proportion like that in Figure 3, and some of the points one can make with a continuous proportion cannot be made with a non-continuous proportion. It is true, e.g., that if XA : AY :: YB : BZ, then (XA)(BZ) = (AY)(BZ), but if XA : AY :: YB : BZ is non-continuous, then nothing follows about the ratios XY : YZ, AY : YB, or XA : BZ.

Plato returns to the epistemological proportion in Book VII, in a passage that looks back at the sun, the line, and the cave, and the psychological and educational points they were enlisted to illustrate:

Dialectic [hê dialektikê] is the only field of inquiry... whose quest for certainty causes it to uproot the things it takes for granted in the course of its journey, which takes it toward an actual starting-point. When the mind's eye is literally buried deep in mud, far from home, dialectic gently extracts it and guides it upwards, and for this reorientation it draws on the assistance of those areas of expertise we discussed [the mathematical sciences, described at 524D7-531D6]. It's true that we've often called them branches of knowledge in the past, but that's only a habit and they really need a different word, which implies a higher degree of clarity than belief has, and a higher degree of opacity than knowledge has. Earlier [at 511D4] we used the word "thought" [dianoia]. But I don't suppose we'll quarrel about terminology when we're faced with matters as important as the ones we're looking into at the moment...

So the terms we used earlier will do.... We'll call the first section knowledge [epistêmê], the second thought [dianoia], the third confidence [pistis], and the fourth conjecture [eikasia]; and the first pair constitute intellect [noêsis] (which is concerned with real being [ousia]), the second pair belief [doxa] (which is concerned with becoming [genesis]). As being is to becoming, so intellect stands to belief; and as intellect stands to belief, so knowledge stands to confidence and thought to conjecture. However, we'd better pass over the proportionate relationships between the objects of intellect and belief, Glaucon, and the twofold division of each of the two realms -- the domain of belief and the domain of intellect -- if we want to avoid getting entangled in an argument which would be many times as long as the ones our discussion has already thrown up. (533C7-534A8)

According to the proportions Plato draws here -- ousia : genesis :: noêsis : doxa :: epistêmê : pistis :: dianoia : eikasia -- with respect to clarity epistêmê (or noêsis in Plato's earlier terminology) is to pistis as dianoia is to eikasia. Ignoring for the moment ousia and genesis, Plato's claim here is that with respect to clarity and unclarity

noêsis : doxa :: epistêmê : pistis :: dianoia : eikasia (534A3-5).

The upshot of 511D6-E4, I have argued, is that

eikasia : pistis :: dianoia : noêsis.

These proportions are equivalent -- A : B :: C : D if and only if D : B :: C : A. So the proportion drawn at 534A3-5 reiterates that drawn earlier at 511D6-E4. Notice that nothing is said about the relationship of dianoia and pistis to each other -- which is just to emphasize the fact that the proportion is non-continuous. Hence the epistemological proportion must be distinguished from the ontological proportion.

Here, then, is another reason to reject the idea that for each term in the epistemological proportion there must be a corresponding term in the ontological proportion. There are three different terms in the first proportion, and four in the second. Plato is now making a different point, using a different kind of proportion.

My third reason for rejecting the idea of a unique ontological correlate for each item in the epistemological proportion is this. As we have seen, Plato suggests that the same things can be treated or used as originals or as likenesses, depending on one's purpose or point of view. Perceptible things around us are treated as originals at 510A5-7; but the mind can also use them as likenesses in order to grasp something intelligible (510B4-5, 510E2-511A1, 511A5-7). In the former case the perceptible things around us are ta pista; in the latter case, used as visible forms, they are ta dianoêta. The same things, then, can be objects of more than one of the epistemic states Plato distinguishes. Likewise, at 511D1-2, in the course of developing the second proportion, Glaucon suggests that on Socrates' view geometers and mathematicians can have nous of the objects of their crafts, if they proceed from a genuine starting-point. Socrates goes along with this. More generally, I see no need to take Plato to be committed to the view that ta doxasta simply cannot be known or understood, that perceptible things are inherently beyond knowledge or understanding. I suggest that what he is claiming here -- and in similar-sounding passages at Rp 475E9-480A12 and 523A10-524D4, and Phaedo 74A2-E4 -- is that unless one understands that it is intelligible forms that constitute perceptible things, and unless one is able to grasp these forms in those things, one cannot understand those things. Perceptible things as such are ta doxasta, not ta gnôsta; but if they are seen for what they are, confused mixtures of forms many of which are not accessible to the senses, they can be ta gnôsta. After all, on Plato's view the dialectically-trained philosopher-king must be able to identify the (intelligible) forms in the (perceptible) things around him (402A7-C8), and he tries to establish, with respect to all things (including, presumably, perceptible things), what each is in itself (533B1-3); and he is able to give an account of everything (including perceptible things) (534B3-4). The dialectician has epistêmê of things of which everyone else has only pistis or doxa (601E7-602A1; cf. 534B8-C5, 520C1-6, 402B5-C8).

The facts (i) that the epistemological proportion is non-continuous, and (ii) that each of the (progressively clearer) states of eikasia, pistis, dianoia, and noêsis is set over a subsection of the divided line, suggest that in higher subsections of the line one has epistemic access to something (or to features or aspects of something) that one has no access to in lower subsections. The line suggests a progression in this sense only: the higher the section, the clearer the state. But since as we have seen Plato never says or implies that there is a one-to-one correspondence between these epistemic states and categories of objects, and since even in the divided line passage itself Plato assumes that the same kind of object can be grasped by different epistemic states, these facts should not be taken to imply that in higher subsections of the line the objects to which one has access are necessarily different. Nothing so far suggests that the divided line should be read as a scale or progression according to which things can be distinguished according to their "form of existence." The divided line does not depict, or provide the basis for, a progression of that sort.

It should be obvious that the ontological and epistemological proportions are not unrelated. Plato's writings are filled with tantalizing suggestions that truth or reality [alêtheia], being [ousia], and understanding [epistêmê] go together in some way. (In the Republic see especially 585C7-12; cf. 478C10-14, 479C7-D1, 518C7-D1, 519A8-B4, 523A1-3, 525C5-6, 526E6-7, 527B5-9, 532C3-D1, 534A3-5; see also Phaedo 65A10-66E2, 78C10-79D7, 82D9-83B4; Theaetetus 186D2-E9; Timaeus 27D5-28A3, 49C7-50A3, 51D2-E5; Philebus 58A1-59D5.) My claim is only that there is no need, on the basis of the divided line analogy, to assume a simple one-to-one correspondence between the terms of the ontological proportion and those of the epistemological proportion, or to assume that for each term of the epistemological proportion there is a unique ontological correlate. The relations between the two proportions are not so simple.

One consequence of the assumption that the terms in the epistemic proportion do have unique correlates in the ontological proportion is the need for something like the "mathematical intermediates" attributed to Plato by Aristotle (see Metaphysics 987b14-18; cf. 1002b14-16, 1090b3-1091a5). For if one makes that assumption, it seems plausible to take Plato to be saying that ta eikasta are likenesses, shadows, and reflections (510A1-3), that ta pista are the perceptible things around us (510A5-7), and that ta noêta or ta epistêta are the forms (511B3-C2). But then what are ta dianoêta?

The foregoing considerations suggest that this is the wrong question to ask. The terms of the second proportion -- noêsis, dianoia, pistis, and eikasia -- are not distinguished by reference to their objects, since more than one state or condition can be set over the same object, or the same kind of object. How then are they distinguished? According to the passage in which the epistemological proportion is drawn, it is by their methods. The practicing mathematician takes for granted the entities with which he works and gives no account of them, but treats them as starting-points; his state or condition is dianoia (510C2-D3). He may deal with forms, e.g. the square itself [tou tetragônou autou] or the diagonal itself [diametrou autês] (510D7-8). But he simply takes them for granted. It is with such an attitude in mind that, after describing the mathematical curriculum in Book VII, Plato says that

[the mathematical sciences] are evidently dreaming about reality. There's no chance of their having a conscious glimpse of reality as long as they refuse to disturb the things they take for granted and remain incapable of explaining them [heôs an hupothesesi chrômenai tautas akinêtous eôsi, mê dunamenai logon didonai autôn]. For if your starting-point is unknown [ho mê oide], and your end-point and intermediate stages are woven together out of unknown material [ex hou mê oiden], there may be coherence, but knowledge is completely out of the question. (533B8-C5)

It is possible, however, to have noêsis or epistêmê of mathematical objects -- they are noêta -- if one starts from an unhypothesized archê (511C8-D5). For this one needs the science of dialectic (511B3-C2, 532A1-533E1). Possessed of dialectically-accessible unhypothesized archai, one's state or condition is nous or noêsis or epistêmê, and it is said to be clearer [saphesteron] than dianoia (511C7). Plato is not concerned in the divided line passage to say how dialectic accomplishes these tasks; but he returns to this later in Book VII, in his description of the education of the rulers, 522C6-534D1.[10]

I have argued in this section (a) that the divided line passage does not offer a single scale or progression according to which things can be distinguished according to their "form of existence," (b) that it is a mistake to think that for each of the epistemic or psychological states Plato introduces at 511D6-E4 there is a unique category of object to which it corresponds, or in other words that for each term in what I have called the epistemological proportion there is a corresponding term in the ontological proportion, and (c) that properly understood the divided line analogy provides no reason to countenance mathematical intermediates -- that the fact that at 511D2-5 Plato introduces a psychological or epistemic condition (dianoia) that is intermediate between noêsis and doxa (= pistis) does not show that he saw the need for a category of things intermediate between the forms and perceptible things.

IV

Another consideration that might lead one to see in the divided line the basis for a scale of things' "form of existence," or "the vertical course leading to the real world," (Sterling and Scott) is the assumption that the divided line -- or at any rate the epistemological proportion -- "corresponds to" or "parallels" the ascent described in the cave parable.[11] In other words, for each term in the epistemological proportion there corresponds a different object, or different category of object, in the cave parable. After all, the chained prisoners see only shadows and hear only echoes (514A3-B6, 515A5-8), and take these shadows and echoes to be what is real and true (515A4-5, 515C1-2). The prisoners who have been unchained but who cannot make it up the rough steep path see the fire and the puppetlike artifacts that cast the shadows on the wall (515C5-D1). They see more correctly [orthoteron blepoi] since what they are seeing is more real [mallon onta], or closer to what is real [mallon to egguterô tou ontos] (515D1-5). Nevertheless, at least until they grow accustomed to these new things, they think the shadows are truer [alêthestera] than what they are now able to see (515D5-7). Those who make it up the path out of the cave and into daylight are initially dazzled; but then they see shadows, then reflections, and finally perceptible things (516A5-8). Eventually they are able to see the night sky, the stars and the moon (516B1-3). Finally, some of those who escaped from the cave are able to catch sight of the sun as it is in itself (516B4-8), and they may come to figure it out that the sun provides the seasons and the years, that it oversees everything in the visible topos, and that it is in a way the cause of everything they used to see (516B9-C3). Such people have reached the final goal of the visible (532B1-2).

Noting this fourfold division, one might expect Plato to link the cave parable to the divided line analogy. What he says is this:

You should apply this allegory, as a whole, to what we were talking about before. The region which is accessible to sight should be equated with the prison cell, and the firelight there with the light of the sun. And if you think of the upward journey and the sight of things up on the surface of the earth as the mind's ascent to the intelligible realm, you won't be wrong -- at least, I don't think you'd be wrong, and it's my impression that you want to hear. Only God knows if it's actually true, however. Anyway, it's my opinion that the last thing to be seen -- and it isn't easy to see either -- in the realm of knowledge is the good; and the sight of the form of the good leads one to deduce that it is responsible for everything that is right and fine, whatever the circumstances, and that in the visible realm it is the progenitor of light and the source of light, and in the intelligible realm it is the source and provider of truth and knowledge. And I also think that the sight of it is a prerequisite for intelligent conduct either of one's own private affairs or of public business. (517A8-C5)

What is perhaps most striking about this passage, given its proximity to the divided line, is that it contains nothing that clearly refers back to the line. It is quite clear that "what we were talking about before," to which the cave image must be connected, is the sun simile, not the divided line analogy. Dwelling in the prison is to be likened to what is accessible by sight [tên men di' opseôs phainomenên] (517B1-3), a clear reference to "the visible realm" in the sun simile (508B13-C2, 508E6-509A5, 509D1-4). The fire within the cave is to be likened to the light of the sun (517B3-4); this echoes 507E4-10, which notes the sun's power to illuminate visible things. We are to interpret the upward journey and the sight of things up on the surface of the earth as the mind's ascent to the intelligible realm (517B4-6). Nothing in either the sun simile or the divided line analogy corresponds to this: the two realms are distinguished in the former, but there is no suggestion that one can move from one to the other; and in the latter the dialectician ascends to a starting-point from hypotheses (511B3-C2), but this ascent takes place within the intelligible section of the line. The rest of the passage, which singles out the form of the good as what is responsible for everything that is right and fine in anything (517B8-C2) and as the progenitor and source of light in the visible realm and of truth and knowledge in the intelligible realm (517C2-4), is a clear echo of the sun simile (especially 508E4-509D3). The closing claim, that intelligent conduct either of one's own private affairs or of public business requires that one must have see the good itself (517C4-5), is also new. Plato is now interested in the ethical and educational ramifications of what he has been saying, and this claim will be developed more fully later in Book VII (534B8-D1, 540A4-B1).

So 517A8-C5 does not support the idea that the cave "corresponds to" or "parallels" the divided line. Still, it might be said, Plato does appear to give us in the cave parable four types or categories of objects: (i) shadows and echoes (515A5-8, 515B7-9); (ii) the puppetlike artifacts that cast the shadows (514B8-515A1); (iii) the perceptible people and animals of which these artifacts are likenesses (516A5-B2); and (iv) the sun as it is in itself (516B4-7). And he might be taken to give us four stages in the ascent from the cave: (i) that of the prisoners chained in the cave (514A2-B1); (ii) that of the unchained prisoners who remain in the cave (515C6-D7); (iii) that of those who see perceptible things by the light of the sun (515E6-516B2); and (iv) that of those who can see the sun itself and who understand its power (516B4-C2). And it is undeniable that at 511D6-E4 Plato distinguishes four states of mind, graduated in clarity and set over subsections of the line that vary correspondingly in truth or reality. It is tempting to conclude that for each of the states of mind there corresponds a (unique) stage in the ascent from the cave and a (unique) category of object:

1. eikasia -- prisoners chained in the cave -- shadows and echoes;

2. pistis -- unchained prisoners who remain in the cave -- artifacts seen by the light of the fire;

3. dianoia -- those who have escaped the cave -- perceptible things seen by the light of the sun;

4. noêsis or epistêmê -- those who can see the sun and understand its power -- the sun as it is in itself.

Neat as this would make Plato's scheme, the temptation must be resisted, for several reasons. First, Plato's parable does not suggest exactly four stages in the ascent from the cave, as Richard Robinson has observed.[12] Second, it does not really present us with exactly four types of object, since Plato mentions also reflections of perceptible things (516A6-7), the moon, stars, and night sky (516A8-B1), reflections of the sun (516B4-5). Third, as we have seen, the relation between eikasia and pistis suggested in the divided line analogy is considerably different from that suggested in (1) and (2) above. Eikasia is not a matter of confusing likenesses and originals (which is what the chained prisoners do: 515A4-5, 515C1-2); it is a matter of using likenesses to arrive at conclusions about (perceptible) originals. Geometers do not mistake visible forms for the forms themselves; the conclusions they draw are about the forms themselves, but are defective for being based on unexamined hypotheses (510B4-511A8). Fourth, (4) suggests that it is the form of the good that is the object of noêsis; the divided line suggests that all forms are objects of noêsis. Even if the form of the good is a stand-in for all forms in the cave parable, it is still the case, as we saw earlier, that according to the divided line forms are not the only objects of noêsis. Objects of one ontological type (perceptible things, e.g., or forms) can be grasped by different epistemic means, and are treated in different subsections of the line. Finally, it is important to notice that the philosophers who succeed in making the ascent Plato describes will be expected to go back down into the cave (520C1-6; cf. 516E3-517A6). Because they have grasped the forms, they will be able "to identify every one of the images and recognize what it is an image of" [gnôsesthe hekasta ta eidôla hatta esti kai hôn, 520C4-5]. What the philosophers have gnôsis of, then, are the very things of which the prisoners have only doxa or pistis. I conclude that the cave parable is not parallel to the divided line in the sense that for each of the terms in the epistemological proportion there corresponds a unique category of object in the cave parable.[13]

V

The ideas that in the divided line analogy Plato is presenting a "scale of reality," that he is contrasting the "intelligible world" and the "sphere of appearances," and that "the line is the vertical course leading to the real world," are common enough. If, as I have argued, Plato is better understood as suggesting two closely related proportions rather than one progression or ascent, the basis for these ideas must be reexamined. What may have suggested these ideas is this. As he develops and comments on the sun, the line, and the cave, Plato repeatedly contrasts a visible [horatos] topos and an intelligible [noêtos] topos (see, e.g., Rp 508C1-2, 509D1-4, 516C1, 517A8-C5, 526E3, 532C7-D1; cf. 524C13, 532A5-B2). The literal meaning of the term "topos" is spatial; it means "place" or "region" or "world." But how literally should we take the contrast between the horatos topos and the noêtos topos?[14] If the point of this contrast were spatial or quasi-spatial, then Plato would be saying that the topos of perceptible things (the "visible world") is distinct and separate from that of the forms (the "intelligible world").[15] There are problems with this view, however. If the forms inhabit a literally different world from our own, if they are "themselves by themselves" [auta kath' hauta] in this strong sense, then they cannot play the sort of causal or explanatory role Plato clearly takes the forms to play. Consider Plato's conception of the explanatory role of forms in the Phaedo: they are taken to be (among other things) entities whose causal powers are responsible for the characteristics and behavior of perceptible things. They are said to be present in, or to have communion with, the things that participate in them; it is because they are in or with or among perceptible things that those things have the characteristics they have (Phaedo 100C-102D, esp. 100C3-E3, 101C1-7, 102B1-D3; cf. Hippias Major 292C9-D6, 293E11-294C7; Laches 191E9-192A6; Lysis 217C3-218A2; Protagoras 332A2-E7; Rp 351D4-352A3, 433B9-C1, 443B4-5; Phaedrus 270C10-E5). Throughout the dialogues -- and not only the early and middle dialogues (see, e.g., Timaeus 35A1-B3, 48A1-2; Philebus 24E7-27C1, 29A9-30C7) -- Plato thinks of the forms as entities with causal and explanatory powers, whose presence in or with or among perceptible things makes these things what they are. Forms located in a literally different world would be unable to do what Plato invokes the forms to do, as he is well aware (see Parmenides 133C3-134E8).

Second, we must remember that the sun, the line, and the cave are images (Rp 509A9, 517A8). As they are developed Glaucon is repeatedly asked to imagine or picture things (508B9, 508D4, 508D10, 514A2, 514B7-8); and they are qualified by some of the most explicit caveats in all of Plato's writing (see 505A1-4, 506C6-D5, 507A1-5, 517B7-C5). Socrates himself warns Glaucon against taking his spatial language too literally at 529A9-C2. So we must not be overly literal in reading what Plato so explicitly cautions is not to be taken as a straightforwardly literal account.

Third, there is no linguistic need to take Plato's usage of "topos" as literally spatial or quasi-spatial. As Jon Moline has pointed out, the Greek of Plato's day offers a number of non-literal senses (or non-spatial uses) of topos: Liddell-Scott-Jones list "commonplace" or "element" (in rhetoric), "opening," "occasion," and "opportunity."[16] So a topos of vision need not be understood as a literally different place than a topos of understanding or thought, and Plato need not be taken as suggesting that the forms occupy a different world, or a different space, than things do.[17]

Consider a roughly contemporary non-Platonic work, the Hippocratic treatise On the Art [Peri Technês]. In section 11, having distinguished between clear diseases [ta phanera tôn nosêmatôn], which can be diagnosed by sight and whose symptoms are evident to perception, and diseases that are less clear [ta hêsson phanera] or obscure [adêla], the author goes on to say that

without doubt no one who sees only with his eyes can know anything of what has been here described. It is for this reason that I have called them obscure.... Their obscurity, however, does not mean that they are our masters, but as far as is possible they have been mastered, a possibility limited only by the capacity of the sick to be examined and of the researchers to conduct research. More pains, in fact, and quite as much time, are required to know them as if they were seen with the eyes; for what escapes the eyesight is mastered by the eye of the mind [hosa gar tên tôn ommatôn opsin ekpheugei, tauta têi tês gnômês opsei kekratêtai] (after W.H.S. Jones)

The author goes on to contrast seeing the problem with one's eyes, or learning of it with one's ears, with tracking it by reasoning [logismôi metêei]. His claim is that there can be no understanding [eidotês, gnômê] of the obscure diseases without reasoning [logismos] or intelligence [sunesis], though opinion [doxa] about them is still possible.

It was pointed out long ago by C.M. Gillespie[18] that the terms "eidos" and "idea" are used throughout the Hippocratic corpus, and by H.C. Baldry[19] that Plato's usage of such technical terms is often based on that of the Hippocratic writers. The point of the author of On the Art is a very Platonic one: understanding does not come through the senses, but only through reasoning. As Plato would put it, perceptible things as such cannot be known or understood; only the forms can be understood.

It would be perverse to argue that, since the causes of obscure diseases cannot be grasped with the senses but only by intelligence or reasoning, they must therefore occupy a world or realm literally separate from the world occupied by the patients suffering those diseases. The author of On the Art clearly is not saying that the causes of obscure diseases are found in a world different from our own; his claim is rather that, while in patients in this world, such causes cannot be grasped by perception but only by reasoning.

Likewise, Plato's distinction between the visible topos and the intelligible topos need not be taken to commit him to the idea that forms occupy a world different from that populated by the perceptible things around us. Perceptible things are of course qualitatively distinct, and they cannot be apprehended by eyesight but only by the understanding. But this does not license talk of two literally different worlds any more than the Hippocratic claim that "what escapes the eyesight is mastered by the eye of the mind" licenses the idea that the practicing physician is not working on flesh and blood patients. The forms or powers the physician is concerned with, which are responsible for the obscure diseases, are in his patients, but they are not accessible to the senses without reasoning or intelligence. So too the forms, including the form of the good, are in the perceptible things around us, but because they are mixed together in confusing ways they (and so the truth about perceptible things) cannot be perceived. They are not perceptible, but only intelligible. The philosopher is able to identify the intelligible forms in the perceptible things around him (402A7-C8; cf. 533B1-3, 534B3-4). This would not be possible if the forms occupied a world different from that populated by the perceptible things around us.

VI

In the divided line passage, I have argued, Plato is making two points. The first he makes by way of an ontological proportion, and it is a thoroughly familiar one. Plato has argued before, most recently at Republic 476A5-479E8, that perceptible things are intermediate between what purely is and what completely is not (478D5-7, 477A9-B1), that they share both in what is and in what is not (478E1-3). And we also know that ta gnôsta (intelligible forms as opposed to perceptible things) are fully what they are (477A3-4), and do not partake of opposites (479B8; cf. Phaedo 74A9-C5, 78C10-79D7). The division of the line into a visible and an intelligible section, then, is just what we should expect. The other ontological claim Plato makes -- that ta doxasta are to ta gnôsta as likenesses to originals -- is not wholly new, since similar claims, though not so general in scope, are made at Symposium 210E5-211B5 and Phaedo 74B4-C1 (cf. 78C10-79A10). This classification is picked up, of course, toward the end of the Republic at 596E4-598D5: the artist's (likeness of a) bed is not as real or as true [alêthê] as the carpenter's bed, which in turn is not completely real [teleôs on] but is somewhat obscure when compared to the truth [amudron to...pros alêtheian] (597A2-10). So there are three forms or kinds [eidê] of beds: the one in nature, the one the carpenter makes, and the one the artist makes (597B5-14). The carpenter looks toward the form in making his bed (596B6-8), the artist looks not toward what is, as it is, but toward what appears, as it appears (598B1-4). Consequently the artist's work is at three removes from what is by nature (597E3-4). It is the kernel of these points that Plato is making, very abstractly, at 509D6-510B1.

Plato goes on, in the rest of the divided line passage, to make an epistemological point, and this is new. The epistemological proportion, eikasia : pistis :: dianoia : noêsis, is a genuine development in Plato's epistemology (reading backwards we can perhaps see hints of it in the discussion of methods of inquiry at Phaedo 95E7-102A1; but they are no more than hints). The rationale for the whole educational program outlined in Republic VII depends on this new development. Plato is now in a position to say something, however tantalizing and incomplete, about the difference between scientific and mathematical methods on the one hand and dialectical methods on the other. It is the differences first articulated in the divided line's epistemological proportion that lead Plato to claim that dialectic is the coping-stone to be placed at the top of the prospective rulers' studies (534E2-3), and that the dialectician, not the scientist-mathematician, sees things whole (537C6-7). The dialectically-trained ruler tries to establish systematically, with regard to all things, what each of them is (533B1-3), and he (or she, 540C5-7) alone can give an account of the being of each thing (534B3-4).

What I have been concerned to argue in this essay is that these two points are distinct, that the divided line analogy does not imply that for each of the four psychic conditions Plato distinguishes and relates in the epistemological proportion there corresponds a separate category of object. If there is a progression in the divided line (a) it is within each of the sections of the line, and (b) it is an epistemic progression without some of the ontological implications it is commonly taken to have.

NOTES

1. The translation I shall use throughout this essay is that of Robin Waterfield, Plato Republic (Oxford, 1993). However, rather than following Waterfield in using "type" to translate Plato's eidos I shall keep the traditional "form"; and I render expressions such as to agathon as "the good" rather than as "goodness." [Back to Text]

2. I am not suggesting that the two proportions are unrelated. They are closely related. The epistemological proportion has evident ontological ramifications. But (a) Plato is not concerned with those ramifications at 510B2-511E5, and (b) these ramifications cannot be made clear by conflating the ontological and epistemological proportions as they are in Grube's diagram. [Back to Text]

3. W.D. Ross, Plato's Theory of Ideas (Oxford, 1953), p. 45. [Back to Text]

4. J.S. Morrison ("Two Unresolved Difficulties in the Line and Cave," Phronesis 22 (1977) writes of 509D6-510A3 that the form of the sentence is irregular owing to its conversational nature, but it is plain enough that the terms that are being related to each other... are on the one hand (men) the two subsections of the visible [AD and DC in Figure 1]... and on the other (but in fact he breaks off before he gets to the other hand) [the two subsections of the intelligible]. He does not say here, or even imply, anything about the relationship of the upper subsection of the visible to the lower subsection of the intelligible. (221)

   It is true that this sentence (509D6-510A3) does not assert any relation between "the upper subsection of the visible" (DC) and "the lower subsection of the intelligible" (CE). But as we have seen, two features of the larger context suggest that DC = CE: (i) the fact that AB is divided in the same ratio as AC and CB, and (ii) the fact that in CE the mind uses as likenesses the same things that in DC were models. [Back to Text]

5. See the discussion of the sightlovers and soundlovers (475E2-480A12), where "doxa" does for Plato what "pistis" is doing here; and compare the discussion of perceptions involving conflicting appearances (523A10-524D4), where some of the limitations of aisthêsis are noted. [Back to Text]

6. To noêton here is the equivalent here of "the realm of knowledge" mentioned at 510A10, and of "the intelligible realm" mentioned at 510B3. [Back to Text]

7. As Thomas Heath points out, Euclid's expression for "continuous proportion" is "hexês analogon," literally "proportional in order, or successively". See The Thirteen Books of Euclid's Elements (New York, 1956), volume 2, p. 293. In A History of Greek Mathematics, I (Oxford, 1921), Heath notes that

   there is...probably little in the whole compass of the Elements of Euclid, except the new theory of proportion due to Eudoxus and its consequences, which was not in substance included in the recognized content of geometry and arithmetic by Plato's time, although the form and arrangement of the subject-matter and the methods employed in particular cases were different from what we find in Euclid. (p. 217) [Back to Text]

8. The Thirteen Books of Euclid's Elements, vol. 2, p. 293; cf. p. 131. [Back to Text]

9. See D.H. Fowler, The Mathematics of Plato's Academy (Oxford, 1987), pp. 8-25 for an account of the importance of this fact. [Back to Text]

10. This is not to say that in these later remarks Plato does clearly say how dialectic accomplishes these tasks. For a good discussion of Plato's obscurity here see Richard Robinson, Plato's Earlier Dialectic (Oxford, 1953), pp. 146-201. [Back to Text]

11. For these expressions see John Malcolm, "The Line and the Cave," Phronesis 7 (1962): 38-45. [Back to Text]

12. Robinson, op. cit., pp. 182-83, writes:

    Evidently the first state is that of viewing the shadows.... Evidently the last state is looking directly at the sun.... But into how many states and changes should we divide the intervening matter? Plato mentions (1) looking towards the light (515C8) and the things going by (D4); (2) looking at the light itself (E1); (3) being dragged out of the cave into the light of the sun (E8); and then looking at (4) shadows (516A6), (5) reflections (A7), (6) things (A8), (7) the nocturnal heavens (A9), (8) the sun (B4). This is certainly not to define a set of changes that would fit precisely between the states enumerated in the Line. Plato's intention seems rather to describe a single continuous change, terminated in both directions, but infinitely divisible within those bounds. He does not seem to be inviting us to rediscover here the four states of the Line.... (p. 182) [Back to Text]

13. Robinson, op. cit., pp. 183-85, argues on the basis of 521C1-D1 and 532A1-D1 that "Plato considered the distinction between [pistis] and [eikasia] irrelevant to the purposes he had in mind in the Cave," and that "the Cave distinguishes the domain of knowledge into the two parts dialectic and mathematics; but it regards the domain of opinion as an undivided unity, represented by the original state of the prisoners." [Back to Text]

14. Jon Moline first impressed on me the importance of this question. See Plato's Theory of Understanding (Madison, 1981), pp. 100-05. The next several paragraphs are indebted to his discussion. I owe the reference to the Hippocratic treatise On the Art to Moline; see pp. 97-100. [Back to Text]

15. Cornford describes "the real existence of the objects of... knowledge -- a world of intelligible 'Forms' separate from the things our senses perceive" as one of the "pillars" of Platonic doctrine (Plato's Theory of Knowledge [Indianapolis, 1957], p. 2). (See also The Republic of Plato, p. xxvii.) E.J. Dijksterhuis writes that "the fundamental idea of [Plato's] entire philosophy is that the things perceived by us are only imperfect copies, imitations or reflections of ideal forms or ideas..., which in a supra-sensible world beyond space and time lead an independent existence that can only be approached by pure thought." (The Mechanization of the World Picture [Oxford, 1969], p. 13.) [Back to Text]

16. Moline, op. cit., p. 101. [Back to Text]

17. LSJ also list as a meaning of topos "sphere" (e.g. "ho pragmatikos topos"), although it is taken from Dionysius of Halicarnassis, an encyclopedist of the first century B.C. This figurative usage captures much of what Plato has in mind throughout the middle books of the Republic: he is contrasting the visible sphere, in which one relies on perception and is at the mercy of conflicting and misleading appearances, and the intelligible sphere, in which one relies on reasoning to get beyond (or behind or underneath) the conflicting appearances to what is really there (see Rp 475E2-480A12, 523A10-524D4; cf. Phd 78C10-79D7, 82D9-83B5, 96A9-100A3; Tm 27D6-28A4, 51D3-52A7). [Back to Text]

18. C.M. Gillespie, "The Use of Eidos and Idea in Hippocrates," Classical Quarterly 6 (1912): 179.-203; also A.E. Taylor, Varia Socratica (Oxford, 1911), pp. 178.-267. [Back to Text]

19. H.C. Baldry, "Plato's Technical Terms," Classical Quarterly 31 (1934): 141.50; also G.F. Else, "The Terminology of the Ideas," Harvard Studies in Classical Philology 47 (1936): 17.-55, especially pp. 18.-21. [Back to Text]

BIBLIOGRAPHY

H. C. Baldry, "Plato's Technical Terms," Classical Quarterly 31 (1934): 141-50.

J.A. Brentlinger, "The Divided Line and Plato's Theory of 'Intermediates'," Phronesis 8 (1963): 146-66.

N. Cooper, "The Importance of Dianoia in Plato's Theory of Forms," Classical Quarterly (n.s.) 16 (1966): 65-69.

F.M. Cornford, "Mathematics and Dialectic in Republic VI and VII," Mind 41 (1932): 38-52, 173-90.

________, The Republic of Plato (New York, 1941).

________, Plato's Theory of Knowledge (Indianapolis, 1957).

G.F. Else, "The Terminology of the Ideas," Harvard Studies in Classical Philology 47 (1936): 17-55, especially pp. 18-21.

A.S. Ferguson, "Plato's Simile of Light," Classical Quarterly 15 (1921): 131-52, and 16 (1922): 15-28.

________, "Plato's Simile of Light Again," Classical Quarterly 28 (1934): 190-210.

J. Ferguson, "Sun, Line and Cave Again," Classical Quarterly (n.s.) 12 (1962): 188-93.

Gail Fine, "Knowledge and Belief in Republic V," Archiv für Geschichte der Philosophie 60 (1978): 121-39.

Robert Fogelin, "Three Platonic Analogies," Philosophical Review 80 (1971): 371-82.

C.M. Gillespie, "The Use of Eidos and Idea in Hippocrates," Classical Quarterly 6 (1912): 179.203.

J.C.B. Gosling, "Doxa and Dunamis in Plato's Republic," Phronesis 13 (1968): 119-30.

G.M.A. Grube, Plato's Republic (Indianapolis, 1974).

R. Hackforth, "Plato's Divided Line and Dialectic," Classical Quarterly 36 (1942): 1-9.

D.W. Hamlyn, "Eikasia in Plato's Republic," Philosophical Quarterly 8 (1958): 14-23.

Henry Jackson, "On Plato's Republic VI, 509d sqq.," Journal of Philology 9 (1881): 132-50.

John Malcolm, "The Line and the Cave," Phronesis 7 (1962): 38-45.

________, "The Cave Revisited," Classical Quarterly (n.s.) 31 (1981): 60-68.

Jon N. Moline, Plato's Theory of Understanding (Madison, 1981), pp. 79-118.

J.S. Morrison, "Two Unresolved Difficulties in the Line and Cave," Phronesis 22 (1977): 212-31.

N.R. Murphy, "The 'Simile of Light' in Plato's Republic," Classical Quarterly 26 (1932): 82-102.

James A. Notopoulos, "The Meaning of Eikasia in the Divided Line of Plato's Republic," Harvard Studies in Classical Philology 44 (1933): 193-203.

________, "Movement in the Divided Line of Plato's Republic," Harvard Studies in Classical Philology 47 (1936): 57-83.

S.B. Pomeroy, "Optics and the Line in Plato's Republic," Classical Quarterly (n.s.) 21 (1971): 389-92.

J.E. Raven, "Sun, Divided Line and Cave," Classical Quarterly (n.s.) 3 (1953): 22-32.

Richard Robinson, Plato's Earlier Dialectic (Second Edition) (Oxford, 1953).

W.D. Ross, Plato's Theory of Ideas (Oxford, 1953).

Nicholas Smith, "The Objects of Dianoia in Plato's Divided Line," Apeiron 15 (1981): 129-37.

R.W. Sterling and W.C. Scott, Plato: The Republic (New York, 1985).

J.L. Stocks, "The Divided Line of Plato Republic VI," Classical Quarterly 5 (1911): 72-88.

C.P. Sze, "Eikasia and Pistis in Plato's Cave Allegory," Classical Quarterly (n.s.) 27 (1977): 127-38.

R.G. Tanner, "Dianoia and Plato's Cave," Classical Quarterly (n.s.) 20 (1970): 81-91.

A.E. Taylor, Varia Socratica (Oxford, 1911), pp. 178.-267.